*내용에 있는 그래프는 방향 그래프(Directed Graph)입니다.
DFS (Depth First Search)
현재 정점과 인접한 간선들을 검사하고, 방문하지 않은 정점으로 향하는 간선이 존재하면 그 간선을 따라서 이동한다. 더이상 갈 곳이 없는 막힌 정점에 도달하면 마지막에 따라왔던 간선을 따라 뒤로 돌아간다.
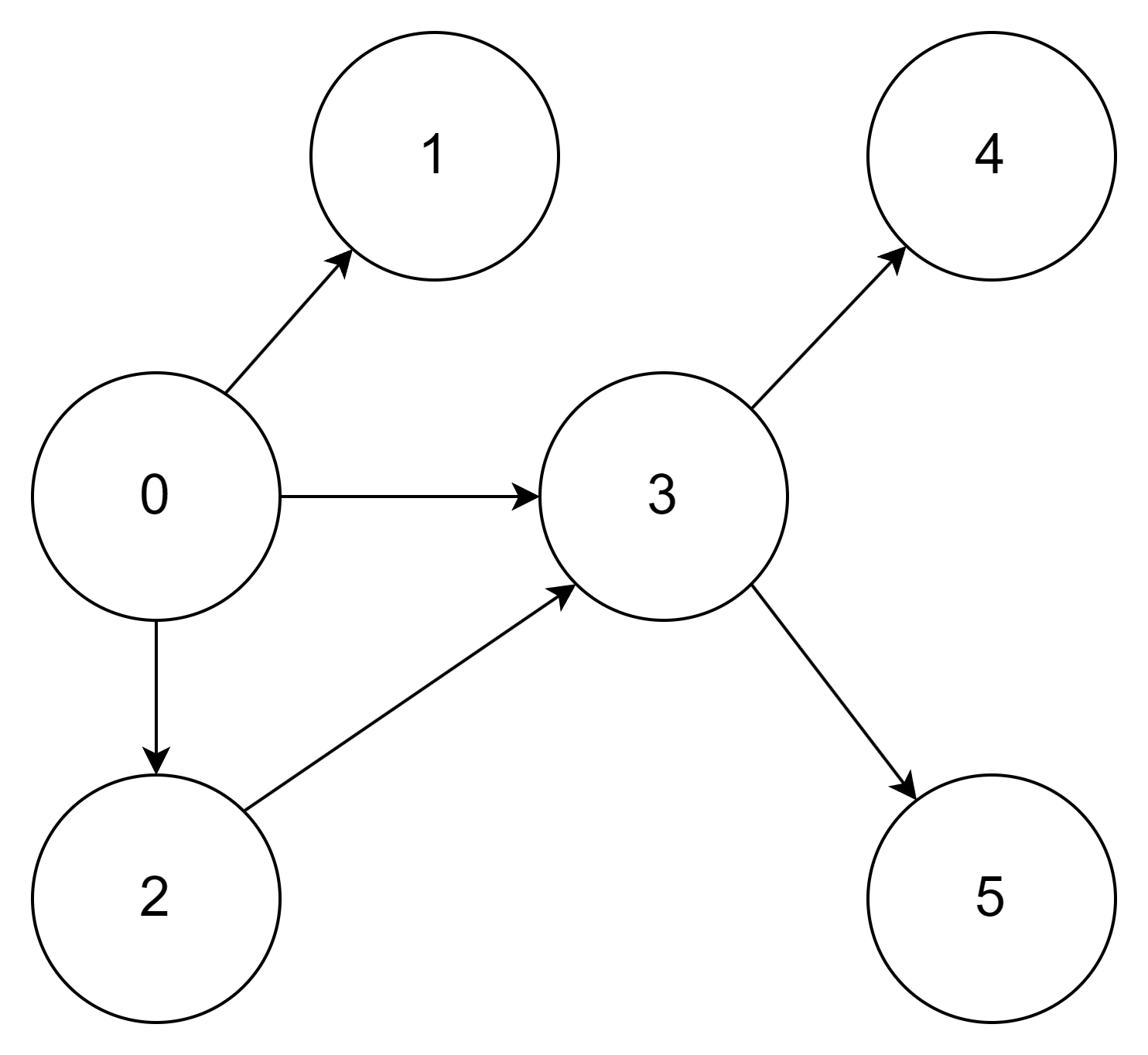
위의 그래프가 있고 출발 지점이 0이라고 했을 때, DFS 과정은 아래와 같다.
| 정점 | 0 | 1 | 2 | 3 | 4 | 5 |
| 방문여부 | X | X | X | X | X | X |
먼저 0에 방문하고, 0과 연결되어있는 정점을 모두 찾는다.

| 정점 | 0 | 1 | 2 | 3 | 4 | 5 |
| 방문여부 | O | X | X | X | X | X |
0과 연결되어있는 정점은 1, 2, 3 이다. 1을 방문한다.
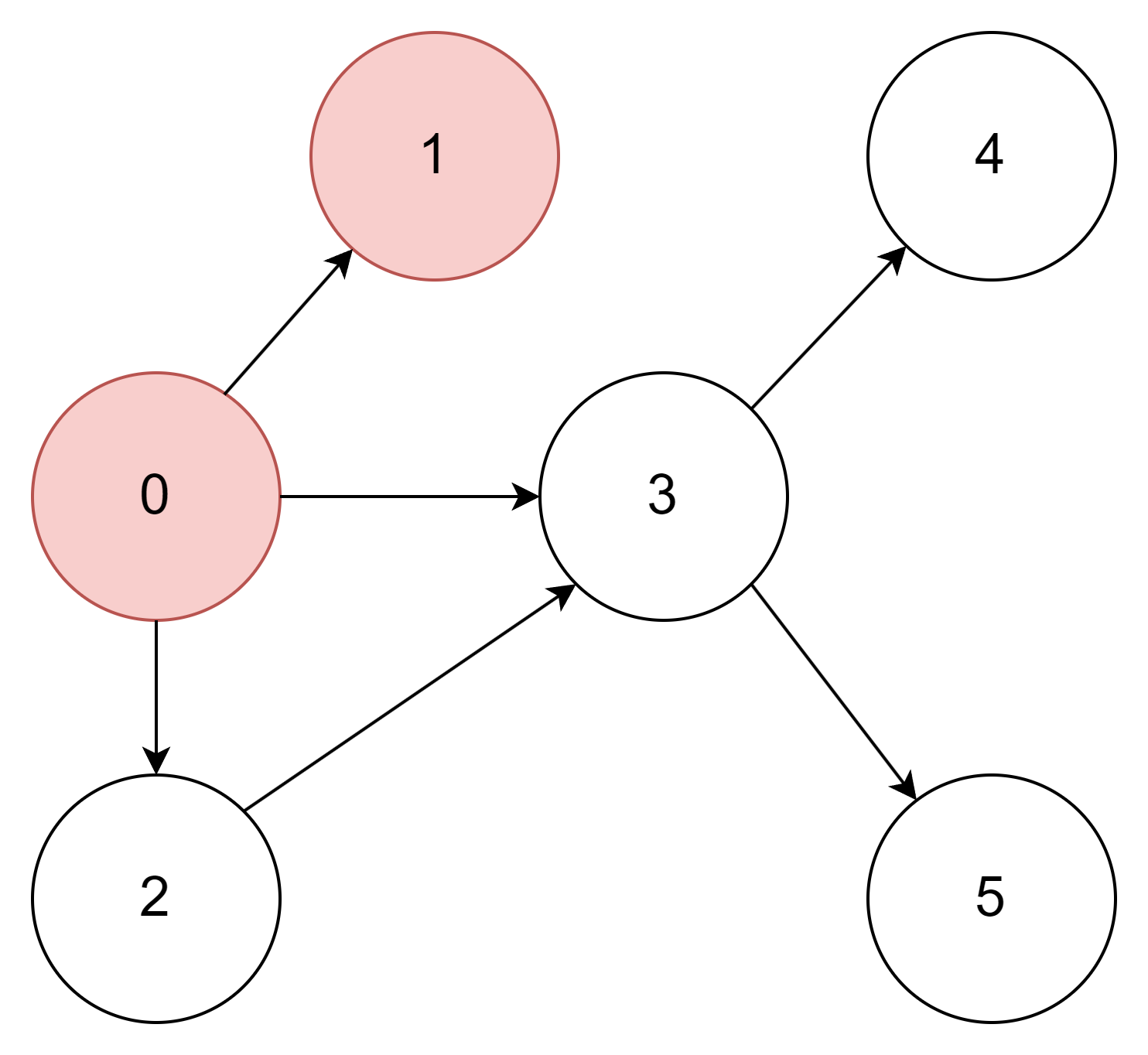
| 정점 | 0 | 1 | 2 | 3 | 4 | 5 |
| 방문여부 | O | O | X | X | X | X |
1과 연결되어 있는 정점이 없으므로 다시 돌아간다.
0과 연결되어있는 정점은 1, 2, 3 이다. (1은 방문했으니 방문하지 않는다.) 2를 방문한다.

| 정점 | 0 | 1 | 2 | 3 | 4 | 5 |
| 방문여부 | O | O | O | X | X | X |
2와 연결되어 있는 정점은 3이다. 3을 방문한다.

| 정점 | 0 | 1 | 2 | 3 | 4 | 5 |
| 방문여부 | O | O | O | O | X | X |
3과 연결되어있는 정점은 4, 5이다. 4를 방문한다.

| 정점 | 0 | 1 | 2 | 3 | 4 | 5 |
| 방문여부 | O | O | O | O | O | X |
4와 연결되어 있는 정점이 없으므로 다시 돌아간다.
3과 연결되어있는 정점은 4, 5이다. 5를 방문한다.
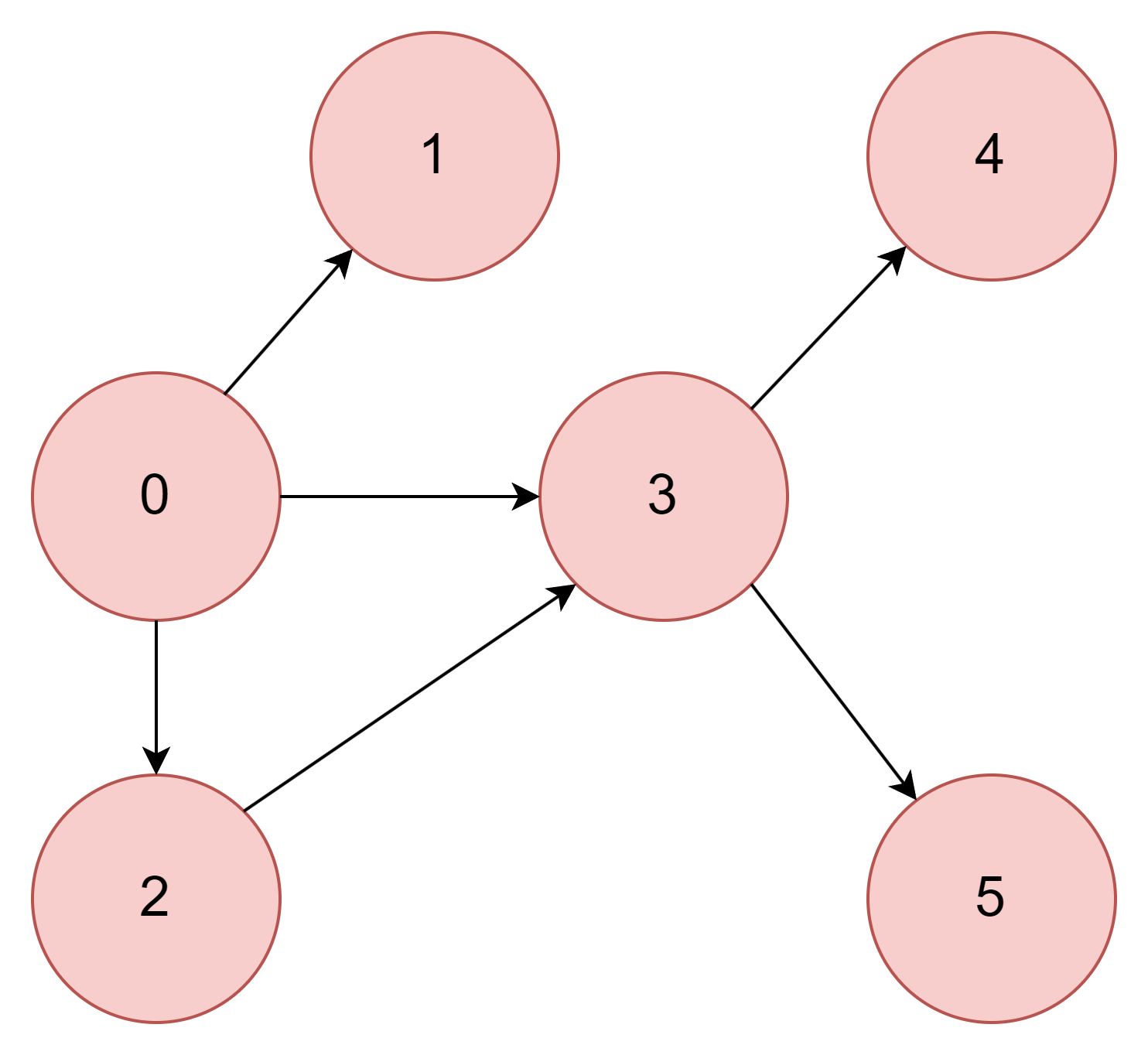
| 정점 | 0 | 1 | 2 | 3 | 4 | 5 |
| 방문여부 | O | O | O | O | O | O |
5와 연결되어 있는 정점이 없으므로 다시 돌아간다.
3과 연결되어 있는 정점을 모두 방문했으므로 다시 돌아간다.
2와 연결되어 있는 정점을 모두 방문했으므로 다시 돌아간다.
0과 연결되어 있는 정점을 모두 방문했으므로 다시 돌아간다. (DFS 종료)
0->1->2->3->4->5 의 순서로 정점을 방문한다.
연결 리스트의 구현에 따라서 순서가 달라질 수 있다.
구현 코드
입력
첫 줄에는 정점의 개수 N, 둘째줄에는 간선의 개수 M이 입력된다.
이후 M개의 줄에 걸쳐서 간선의 정보 I J가 주어진다. I J는 정점 I에서 J로 가는 간선을 의미한다.
6
6
0 1
0 2
0 3
2 3
3 4
3 5
인접 행렬을 이용해 구현한 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class DFSWithAdjMatrix {
// 정점의 방문 여부를 나타내는 배열 visited
// false면 방문하지 않은 정점이고, true면 방문한 정점이다.
static boolean [] visited;
// 그래프의 인접 행렬 표현
// adjMatrix[i][j] = true 라면 정점 i에서 정점 j로 가는 간선이 존재한다는 의미이다.
static boolean [][] adjMatrix;
// 정점의 개수
static int N;
// DFS 결과를 출력하기 위한 StringBuilder
static StringBuilder sb = new StringBuilder();
// 깊이 우선 탐색
private static void dfs(int current) {
visited[current] = true;
sb.append(current).append(" ");
for (int i=0; i< N; i++){
if (adjMatrix[current][i] && !visited[i]){
dfs(i);
}
}
}
// 모든 정점을 방문
private static void dfsAll(){
for (int i = 0; i < N; i++) {
if (!visited[i]){
dfs(i);
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
visited = new boolean[N];
adjMatrix = new boolean[N][N];
int M = Integer.parseInt(br.readLine());
for (int i = 0; i < M; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adjMatrix[from][to] = true;
}
dfsAll();
System.out.print(sb);
}
}출력
0 1 2 3 4 5
인접 리스트를 이용해 구현한 코드 (List)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
public class DFSWithList {
// 정점의 방문 여부를 나타내는 배열 visited
// false면 방문하지 않은 정점이고, true면 방문한 정점이다.
static boolean [] visited;
// 그래프의 인접 리스트 표현
// adjList[i]에는 정점 i에서 갈 수 있는 다른 정점들이 입력 순서대로 들어있다.
static List<Integer> [] adjList;
// 정점의 개수
static int N;
// DFS 결과를 출력하기 위한 StringBuilder
static StringBuilder sb = new StringBuilder();
// 깊이 우선 탐색
private static void dfs(int current) {
visited[current] = true;
sb.append(current).append(" ");
for (int i=0; i< adjList[current].size(); i++){
if (!visited[adjList[current].get(i)]){
dfs(adjList[current].get(i));
}
}
}
// 모든 정점을 방문
private static void dfsAll(){
for (int i = 0; i < adjList.length; i++) {
if (!visited[i]){
dfs(i);
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
visited = new boolean[N];
adjList = new List[N];
for (int i = 0; i < N; i++) {
adjList[i] = new ArrayList<>();
}
int M = Integer.parseInt(br.readLine());
for (int i = 0; i < M; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adjList[from].add(to);
}
dfsAll();
System.out.print(sb);
}
}출력
0 1 2 3 4 5
인접 리스트를 이용해 구현한 코드 (Node)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class DFSWithNode {
// 정점의 방문 여부를 나타내는 배열 visited
// false면 방문하지 않은 정점이고, true면 방문한 정점이다.
static boolean [] visited;
// 그래프의 인접 리스트 표현
// adjList[i]에는 정점 i에서 갈 수 있는 다른 정점들이 입력 순서의 역순대로 연결되어있다.
static Node [] adjList;
// 정점의 개수
static int N;
// DFS 결과를 출력하기 위한 StringBuilder
static StringBuilder sb = new StringBuilder();
// 그래프의 정점
static class Node {
int vertex;
Node link;
public Node(int vertex, Node link) {
this.vertex = vertex;
this.link = link;
}
}
// 깊이 우선 탐색
private static void dfs(int current) {
visited[current] = true;
sb.append(current).append(" ");
for (Node temp = adjList[current]; temp!=null; temp=temp.link){
if (!visited[temp.vertex]){
dfs(temp.vertex);
}
}
}
// 모든 정점을 방문
private static void dfsAll(){
for (int i = 0; i < adjList.length; i++) {
if (!visited[i]){
dfs(i);
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
visited = new boolean[N];
adjList = new Node[N];
int M = Integer.parseInt(br.readLine());
for (int i = 0; i < M; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adjList[from] = new Node(to, adjList[from]);
}
dfsAll();
System.out.print(sb);
}
}출력
0 3 5 4 2 1
참고)
인접리스트 두 가지 코드의 결과가 다른 이유는 List로 구현한 인접 리스트의 경우 0 -> 1-> 2-> 3의 순서로 인접 리스트가 연결되고, 노드로 구현한 인접 리스트의 경우 0-> 3-> 2-> 1의 순서로 인접 리스트가 연결된다.
따라서 노드로 구현한 DFS는 3->2->1의 순서로 탐색하기 때문에 순서가 다르다.
방향이 없는 무향 그래프로 구현하고 싶은 경우
main 메서드의 입력받는 부분을 아래와 같이 수정하면 된다.
인접행렬로 구현한 경우
for (int i = 0; i < M; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adjMatrix[from][to] = true;
adjMatrix[to][from] = true;
}
인접리스트로 구현한 경우 (List)
for (int i = 0; i < M; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adjList[from].add(to);
adjList[to].add(from);
}
인접리스트로 구현한 경우 (Node)
for (int i = 0; i < M; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adjList[from] = new Node(to, adjList[from]);
adjList[to] = new Node(from, adjList[to]);
}Github
https://github.com/jxixeun/Algorithm/tree/master/src/graph
GitHub - jxixeun/Algorithm: 알고리즘을 정리합니다
알고리즘을 정리합니다. Contribute to jxixeun/Algorithm development by creating an account on GitHub.
github.com
'알고리즘 > 개념 정리 (알고리즘 문제 해결 전략)' 카테고리의 다른 글
| 그래프 알고리즘 - 입력 받기 (0) | 2023.04.10 |
|---|
